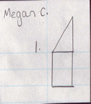 ...this is correct!
...this is correct!
Visualization activities fit well into the oral and mental starter for a lesson. Here is an example of one you might read slowly to a Year 6 class (or higher ability Year 5).
Read through the visualization activity. Try to visualize the shape yourself. The children might benefit from sitting with their eyes closed, though some will prefer to keep their eyes open.
Imagine a square-based pyramid made out of plasticine in the air in front of you. Ask yourself a few questions (but keep the answers to yourself).
How many corners, or vertices, has the shape?
How many edges?
How many faces? Are the faces all the same shape?
Now imagine a cube, with square faces the same size as the base of your pyramid, also floating in space.
Slide your pyramid until it sits on top of the cube, with its base exactly in line with the top of the cube. Ask yourself some questions about the new solid:
How many vertices has it?
How many edges?
How many faces? Are they all the same shape?
Now imagine a sharp knife and use it to make a vertical cut through your solid.
Pull the two halves apart without turning them.
Without saying anything, open your eyes and sketch (or draw, with a ruler) either part as you see them facing you.
You could also try sketching (or drawing) the face created by your vertical cut.
Now, compare your drawing with others.
Check your solution…
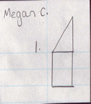 ...this is correct!
...this is correct!
 ...this is too!
...this is too!  ...this is a good attempt at sketching the face created by the vertical cut.
...this is a good attempt at sketching the face created by the vertical cut.
You might think that visualization is just another word for fantasising. In a way, it is – only when we use visualization in mathematics, it’s for a practical purpose.
Visualizing shapes and spaces helps us to gain a very real idea of what is where!
Once you get used to using such a method, you’ll find that it has many everyday uses. For example…
As you can see, there are many uses for visualization methods not only in mathematics, but in day to day life too.
You’ll probably find that you can use the same methods in other school subjects – if you don’t already do so.
Try finding a use for visualization in each of your other curriculum subjects. And if you do, share your ideas with others!
I've used visualization to some degree in other subject areas, and to different ends. Teaching a Year 4 class who were a little boisterous (to say the least) on a windy Friday afternoon, I tried meditation as a technique to calm and re-focus them.
Doing this in the classroom, with the usual distractions, wasn't entirely successful, so we all went out onto the playing field, chose a quiet, sunny spot, and meditated there. I allowed the children to choose whether to sit or lie, and we explored different methods of relaxing and trying to empty our minds.
This was much more successful, and made a noticeable difference to the children's behaviour and work.
Literacy lends itself to visualization, notably in poetry work where listening- rather than visual skills are required. Reading the text of a poem by Dylan Thomas or Gerard Manley Hopkins is fair and well, but ask the children to listen to the poems with their eyes closed, concentrating on alliteration and assonance, and it is a wholly different - enriched - experience. Better still, play a recording of Dylan Thomas reading his poems, and be transported to a magical place!
Obviously, visualization can be used to great effect in Art, and Design / Technology, where accurately imagining images in 2D or 3D is paramount.
Keep the idea and methods learned as you go along in your head, and try to apply them whenever you get the opportunity. It's a valuable, and productive, way of teaching and learning.
ESDGC is a subject ripe for exploiting visualization within. There are a number of Guided Visualisations on sites such as esd-wales.
(From: http://standards.nctm.org/)
Beginning in the early years of schooling, students should develop visualization skills through hands-on experiences with a variety of geometric objects and through the use of technology that allows them to turn, shrink, and deform two- and three-dimensional objects. Later, they should become comfortable analyzing and drawing perspective views, counting component parts, and describing attributes that cannot be seen but can be inferred. Students need to learn to physically and mentally change the position, orientation, and size of objects in systematic ways as they develop their understandings about congruence, similarity, and transformations.
One aspect of spatial visualization involves moving between two- and three-dimensional shapes and their representations. Elementary school students can wrap blocks in nets - two-dimensional figures, usually made of paper, that can be folded to form three-dimensional objects - as a stap toward learning to predict whether certain nets match certain solids. By the middle grades, they should be able to interpret and create top or side views of objects. This skill can be developed by challenging them to build a structure given only the side view and the front view. Middle-grades and secondary school students can be asked to find the minimum number of blocks needed to build the structure. High school students should be able to visualize and draw other cross-sections of the structures and of a range of geometric solids.
visualisation visualization 3D shapes 3 D shapes 3-D shapes primary maths primary mathematics shape space
Last updated April 2006.